ロジカルシンキングとは。思考の整理方法やフレームワーク、ビジネスへの活かし方に迫る
ビジネスシーン・面接などで有益な思考法に、「ロジカルシンキング」があります。
ロジカルシンキングをうまく活用できれば、ビジネスにおける課題解決や企画立案などさまざまなシーンで役立ちます。
ただ、ロジカルシンキングの基本的な概念や活用方法を熟知しておかなければ、効果的な活用は困難です。
そこで本記事では、ロジカルシンキングの基本的な概念・ビジネスでの活用方法を解説します。
ビジネスシーンでロジカルシンキングを駆使したいと考えている方は、ぜひ参考にしてください。
ロジカルシンキングとは
ロジカルシンキングとは、物事の因果関係や包含関係に基づいて筋道立てて考える思考法のことです。
ここでは、ロジカルシンキングの概要と利用するメリットについて解説します。
ロジカルシンキングを理解する上で重要な「論理」と「直感」
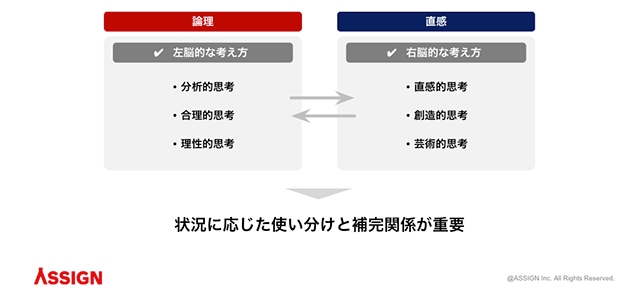
人間の思考法は「論理(左脳)」と「直感(右脳)」に大別されます。
ビジネスシーンで成果を上げるには、この左脳の力と右脳の力を両方とも活用しなければなりません。
上記の図にあるように、論理と直感では得意とする思考が異なります。
直感は、自身の経験則や感覚から答えを導き出すのが特徴です。
経験則や感覚を用いた直感は、サマリーを導く速さに優れており、特に以下の項目について強みを発揮します。
- 大規模な課題
- 変更が必要な事柄
- 即時に行動を起こすべき事項 など
しかし、新規事業の立案や定型業務には強みを発揮しにくい傾向があります。
一方で、新規事業・定型業務で強みを発揮するのが論理です。
論理はデータや事実をもとに理性的に分析し、合理的な判断を下します。
しかし、論理にも弱点があり、例えば数式を用いて考える際に計算ミス一つで大きく異なる結果を導き出してしまう可能性がある点です。
論理・直感ともに得手不得手があるため、互いを補完しながら使い分ける必要があります。
ロジカルシンキングのメリット
ロジカルシンキングのメリットは、以下の2点です。
- 人の感覚で捉えにくいものに対して対処できる
- 構造的に理解するのに役立つ
人の感覚で捉えにくいものに対して対処できる
新規事業を立ち上げるにあたって、「市場規模はどれくらいか」「何人がどれぐらいの単価感でそのサービスを使ってくれそうか」などを検討しなければなりません。
こういった市場規模・見込み顧客の数や単価などの予想は、直感よりも論理のほうが遥かに強い領域です。
例えば、市場のシェア率が1%のものと2%のものがある場合、これは人の感覚としてはほとんど変わらないように感じます。
しかし、営業プロセスにおける移行率・解約率などの指標で考えると、結果として数字は2倍異なることになります。
1%と2%という非常に小さい数字であるがゆえに、直感では捉えにくいですが、論理を用いることでその重要性や数値の意味を正しく理解できるようになるのです。
このようにロジカルシンキングは、人の直感では捉えにくい事象に対し、明確なデータを踏まえて可視化できるというメリットがあります。
構造的に理解するのに役立つ
ロジカルシンキングは、課題を構造的に理解するのに役立つ思考法です。
例えば、売り上げの拡大に向けて明確な指標・目標がないまま取り組むのは、非効率であり芳しい結果が出ません。
売り上げを上げたいなら、「顧客単価」と「顧客数」に課題を分割すると、どちらに対してアプローチをすべきかが明確になります。
また、課題を構造的に分割すると組織内における目的意識の共有が容易になり、議題として取り上げやすくなるのも利点です。
このように、ロジカルシンキングを使って物事を構造的に分解することで、より問題点を明確に把握できたり、解決までの道筋が理解できたりします。
思考を整理する3つの方法
ロジカルシンキングを最大限に活用するためには、代表的な思考の整理方法を理解しておくことが望ましいです。
- MECE
- ロジックツリー
- はしごの構造
MECE:モレなくダブりなく

MECE(Mutually Exclusive, Collectively Exhaustiveの略語)は、全体を構成する要素について「漏れなくダブリなく」整理できる手法です。
全体をいくつかの部分に分けたときに、「分けられた部分が全体を網羅しているか・重複がないか」を確認する際にMECEは用いられます。
【ダブりの例】
人の身長を分類する際「人の身長が170センチ以上か、それ未満か」とする分類は、漏れなくダブリなく分けられている。
しかし、「170センチ以上か、175センチ以下か」とする分類は、170センチから175センチまでが重複しているため、ダブりがある。
【漏れの例】
肉の専門店の出店を想定する際、メジャーな「牛」「鶏」「豚」は思いつきやすいが、「馬」「羊」などは漏れやすい。
漏れなくダブリなく全ての可能性を考慮するためには、要素を細かく分解して考えることが重要です。
MECEは、ビジネスにおける課題解決のシーンで、有益と思われる要素を漏れなくダブりなくリストアップするのに有益な整理法といえます。
ロジックツリー
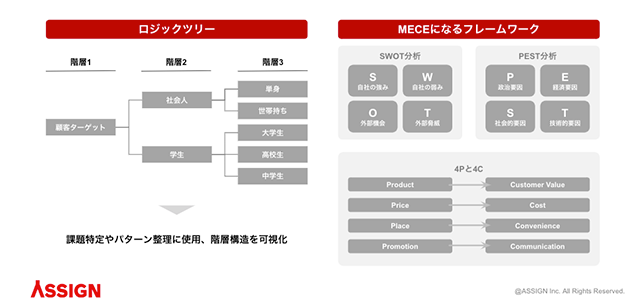
ロジックツリーは、ツリー構造を使って検討対象となる問題を論理的に分解していく整理法で、コンサル業では「イシューツリー」とも呼ばれています。
ロジックツリーを使って、対象のものを分解していく際に便利なのが、MECEになる4つのフレームワークです。
【詳細】
| フレームワーク | 概要 |
| SWOT分析 | 課題に関する内部環境と外部環境を、自社の強み(Strength)・自社の弱み(Weakness)・外部機会(Opportunity)・外部脅威(Threat)に整理して分析する手法 |
| PEST分析 | Politics(政治要因)・Economy(経済要因)・Society(社会的要因)・Technology(技術的要因)の4つの観点から外部環境を分析する手法 |
| 4P | マーケティング施策をProduct(製品・サービス)・Price(価格)・Place(流通)・Promotion(販促活動)の4つの観点から検討する手法 |
| 4C | 顧客目線のマーケティング施策をCustomer Value(顧客価値)・Cost(コスト)・Convenience(利便性)・Communication(コミュニケーション)から検討する手法 |
ロジックツリーを使って分解する際にフレームワークを用いることで、MECEさを担保できます。
はしごの構造
はしごの構造は、問題を深く掘り下げることで、最終的に目指すべき解決策にたどり着くための手法です。
コンサルスキルの一部と捉えられることもあります。
はしごの構造という名称は、問題の深掘りを「下への動き」、検証を「横への動き」としたとき、繰り返すことで形成される形がはしごの形状をしていることが語源です。
はしごの構造を用いた問題の深堀りと、解決策の検討を繰り返す一連の流れを「自社の売り上げが上がらない課題を考えるとき」を例に解説します。
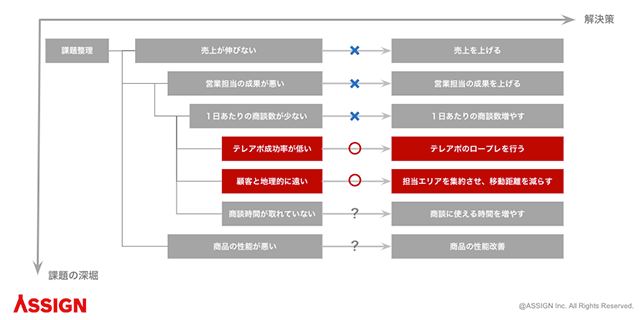
| 【例の解説】 課題「売り上げが上がらない」の解決策は「売り上げを上げる」になりますが、これでは具体性がないため解決策に適していません。 そこで、「なぜ売り上げが上がらないのか」を深掘りして、見つかった原因に対し一つひとつ解決策を検討します。 深掘りして出てきたのが「営業担当の成績が悪い」「1日あたりの商談数が少ない」です。 しかし、「営業担当の成績が悪い」の解決策は「成績を上げる」、「1日あたりの商談数が少ない」の解決策は「商談数を増やす」ですので、まだ具体性のある内容とはいえません。 そこで「なぜ1日あたりの商談数が少ないのか」を深掘りすると、「テレアポの成功率が低い」「地理的にクライアントが離れていて、1日の商談数に限界がある」という課題感が出てきます。 その解決策を考えていくと、「テレアポの成功率が低い」なら「ロープレを行う」、「地理的にクライアントが離れている」なら「担当エリアを集約する」といった具体性のある解決策が見つかります。 こうした具体性のある解決策が出てきたら、ようやく課題解決に動くことが可能です。 |
実際の業務では、上記のような流れで最終的にたどり着いた解決策が、実態に合わず採用できない可能性があります。
採用できない場合は、一つ前の課題に戻って再度深掘りをしたり、解決策が見つかった課題をさらに深掘りしたりすることで、新たな解決策を模索していきます。
はしごの構造を理解する最大のメリットは、何か課題が出たときにそれをスピーディーに解決するためのフレームワークを作成できる点です。
さらに、フレームワークの作成に慣れれば、解決策を考えるときは原因を深掘りすることで、解決策として成立する感覚を掴めます。
はしごの構造は、特に解決策の提示を求められるクライアントワークに従事する人に有益な整理法です。
論理関係を把握するポイント
論理関係を把握するには、「因果関係」と「必要十分条件」の概要を理解しておく必要があります。
ここでは、因果関係・必要十分条件の概要を解説します。
因果関係とは
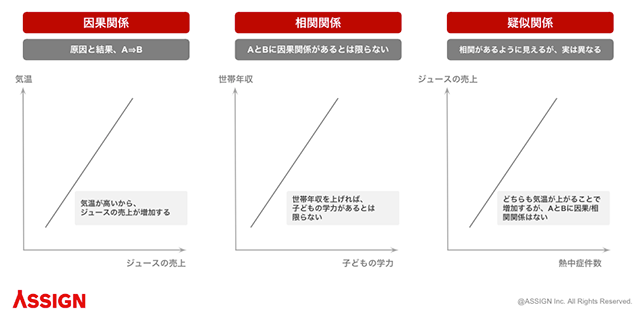
因果関係は、ある事象Aが原因で事象Bに影響がある状態を指します。
影響するパターンは、一次関数的・二次関数的・反比例などケースバイケースです。
この因果関係に似た概念として「相関関係」があります。
相関関係とは、事象Aと事象Bになんらかの関連性がある関係のことです。
また、数学的・統計的な観点では、「Aが増加するとき、Bが増加もしくは減少する傾向が認められる2つの量の関係」を指します。
相関関係の例は以下の通りです。
- 雨が降ると川が増水する
- 時給制の仕事で長時間働くと給料が増える
- 世帯年収の高い家庭の子どもは学力が高い など
相関関係を理解する上で注意すべきなのが、相関関係は必ずしも因果関係を意味するとは限らない点です。
先に挙げた例でいえば、世帯年収の高い家庭の子どもが学力が高いとしても、世帯年収以外に理由がある可能性は捨てきれません。
ほかに原因・理由が考えられる関係性は、因果関係として断定できないのです。
この因果関係を理解する上で重要な概念が「疑似相関」です。
疑似相関とは、因果関係がない関係性にもかかわらず、因果関係があるように見えてしまう相関関係のことを指します。
例えば、「高血圧の人は高収入」といった内容がデータとして判明した場合、一見高血圧が高収入に影響している因果関係があるように見えます。
しかし、実際は高血圧の人は年齢層が高い人の割合が多く、その年齢層は高い役職に就いている割合が多いため、結果として高収入となるのです。
相関関係のなかに年齢・性別のような「第3の変数」が含まれている関係性は、疑似相関となる傾向があります。
ある関係性を因果関係と断定するには、どの要素とどの要素の間に実際の因果関係が存在するのかを正確に把握することが重要です。
因果関係の実例
ビジネスにおける因果関係で真の原因が何かを見誤ると、改善はおろか悪化する恐れがあります。
そのため、慎重かつ正確に真の原因を特定しなければなりません。
因果関係に関する実務的な例を、営業に関わる内容で紹介します。
| 「商談を設定したにもかかわらず、お客様がその商談に実際に現れる確率が低い」 考えられる因果関係は、アポイントメントを取った際のコミュニケーションが悪いことである |
上記の例と考えられる因果関係は、100%成立しているとは証明できませんが、高い確率で成り立つ仮説といえます。
一方で、「アポイントメントから次の商談に移ったものの、提案後の受注率が低い」という原因を「提案内容が悪い」とするのは早計です。
なぜなら、ほかに以下の原因が考えられるからです。
- ターゲットセグメントの選定が間違っていた
- 営業パフォーマンスが低かった
- ヒアリングの内容が不十分だった
- ヒアリングをもとにした提案内容が不適切だった など
上記のように複数の原因が考えられる場合は、一つの原因を因果関係とする強度が弱くなります。
ビジネスにおける事象では、一見因果関係があるように見えた場合でも、第一にほかの要因が影響している可能性を考慮するのが大切です。
そして、事象に対する要因を総合的に洗い出せれば、ロジカルシンキングをうまく活用できていることになります。
必要十分条件

必要十分条件とは、「Aであれば必ずBが成り立つが、Bが成り立つからといって必ずしもAが成り立つわけではない」とされる概念のことです。
ビジネスにおける必要十分条件の例は、以下の通りです。
| あるメールマガジンのタイトルを、AパターンとBパターンの2種類を作成。Aパターンは先月試し、今月はBパターンを試した。その結果、Bパターンのほうが成果がよかった。 サマリー:BパターンがAパターンより優れているとはいえない。なぜなら、Aパターンを試した時期がオフシーズンで、Bパターンを試した時期がピークシーズンであった場合、Bパターンが有利な状況で行われていた可能性があるため。 |
上記の例のように、結果だけで短絡的に捉えるのは事実と異なる可能性があることを留意しておくべきです。
ビジネスシーンでは、頻繁にこの必要十分条件が適用される事象が起きるため、結果だけを見て判断しないように心がけてください。
必要十分条件の実例
ビジネスでは、「必ず成り立つものなのか」「必ずしも成り立つとは限らないものなのか」の2つの観点を持つことが重要です。
先述したメールマガジンの例では、Bパターンの成果がAパターンよりよかった理由はピークシーズン以外にも複数考えられます。
何か事象が起きたときに、その原因を説明できる要因は何パターンあるのかを検討できれば、必要条件や十分条件を見極められます。
ロジカルシンキングで数字を使いこなすには
ロジカルシンキングは、数字を使って物事を整理するときにも役立ちます。
数字を使うメリットは、言語や感覚に流されず、厳密に考えられる点です。
例えば、「市場規模が大きそう」「インパクトが大きそう」などは直感的な判断となり、根拠に乏しいと言わざるを得ません。
印象が実態に即しているのかを、ユーザー数や単価などの具体的な数字で計算すれば、論理的に検証できます。
数字を扱う上で重要となるポイントは以下の2点です。
- シンプルな式への分解
- ドライバーを特定
シンプルな式への分解
数字を扱うにあたって、複雑な分析や多くのデータを収集するシーンが多々あります。
複雑なデータをロジカルシンキングに活用するには、できるだけシンプルな式に分解することが重要です。
例えば「この数字になるためには、何かける何になるか」を考える、つまり掛け算に分解して考える方法があります。
例:「顧客単価」×「顧客数」
ただ、分解により見るべき数字が細かくなりすぎると分析しにくく、数字に踊らされてしまうこともあります。
分解して出た数字に対しては、どのパラメータが固定値(変えることが難しい値)で、可変値(変わる可能性がある値)はどの数字なのかを把握してから活用するようにしてください。
ドライバーを特定
課題を「顧客単価」×「顧客数」などのシンプルな式に分解を行うと、改善すべき値が出てきます。
全て改善するのがベストではありますが、現実問題としてはそうもいきません。
「最終的に向上させたい複数の数字に対して、どの数字の改善に着手することが一番効果的なのか」を特定することを、ここでは「ドライバー」と呼びます。
ドライバーの例は以下の通りです。
| 「今月あと何件の契約が取れそうか」という問いかけに対して、「1社です。おそらくA社と契約できると思います。」と回答をする人が多い。 しかし、この回答だと説得力に欠ける。 これまでの経験則的な感覚に加えて、「3社に提案済みで、今までの成約率から考えて、このフェーズから33%の確率で1社は契約できる」のような説明ができると、より正確で説得力が増すものとなる。 |
説明の段階で、複数の数字からどの数字をドライバーとして絞り込むのかを適切に判断できると、効率的な改善が可能となります。
小さな数字を見落とさない
小さな数字は、人間の感覚としてはインパクトに欠けるため軽視されがちです。
しかし、事業においては小さな数字ほどインパクトが大きいことがあります。
小さな数字でインパクトが大きい例は以下の通りです。
| 1%と2%の違いは感覚的にわかりにくく、軽視しがちである。 しかし実際には、1%から2%に変わるだけで2倍のインパクトがある。 |
1%の確率の場合は、上限にもよるものの2倍以上の余地があることを意味しています。
そのため、改善ポテンシャルや結果への影響が大きい「小さな数字」に注意する必要があるのです。
ロジカルシンキングはビジネスのさまざまなシーンで活用できる
ロジカルシンキングにおける構造的に物事を整理する力・数字で物事を考え原因を深掘りして解決策に移す力・因果関係を把握する力は、さまざまな活用場面があります。
実際の業務では、ロジカルシンキングは以下の場面で活用できます。
- 事業改善
- タスク管理
- ドキュメンテーション
- わかりやすく伝えるためのコミュニケーション など
上記のタスク管理でいえば、大きな分類とともにタスクを羅列すると、漏れに気づきやすくなったり、ほかの事柄を記憶する余裕が生まれたりするメリットが得られます。
ただ、ロジカルシンキングは、すぐに最大限活用するのは難しい思考法です。
それでも、自分に合った部分から少しずつでも事業や実務で活用することが、ビジネスの成功への近道となります。
ぜひ本記事を参考にして、自身の業務に役立ててください。
ASSIGN
アサインはビズリーチの最高ランク受賞等、確かな実績を持つエージェントと、若手ハイエンド向け転職サイト『ASSIGN』であなたのキャリアを支援しています。 コンサルティング業界専門のキャリア支援から始まり、現在ではハイエンド層の営業職・企画職・管理職など幅広い支援を行っています。 ご経験と価値観をお伺いし、目指す姿から逆算したキャリア戦略をご提案し、ご納得いただいた上で案件をご紹介するのが、弊社のキャリア支援の特徴です。
